스터디-ing/AI
[Deep learning] Overshooting & Overfitting
몽상현
2025. 1. 21. 18:00
출처: https://youtu.be/1jPjVoDV_uo?si=bRQcbTuBp63jmr2Z
딥러닝을 공부하던 중 헷갈리는 내용이 있었는데,
너무나도 감사하게 Sung Kim이라는 유투버님께서 정리를 깔끔하게 해주신 영상을 찾게되어 내용을 정리해본다,,
세상 감사합니다,, 이런분들 복받아야해여,, 😍
Overshooting
- 목표 출력 값이나 기준 값을 초과하는 현상.
- 신경망이 학습 과정에서 과도하게 큰 값을 예측할 때 발생.
- 원인
- 학습률이 너무 클 경우, 매 학습 단계마다 모델의 가중치가 과도하게 업데이트 되어 목표 값을 초과하는 예측을 하게됨. → 적절한 학습률(learning rate) 필요
- 적절한 규제(L2 Regularization, Dropout 등) 부족
- 훈련 데이터와 검증 데이터의 분포가 급격히 다를 경우, 예살치 못합 입력에 과도한 반응을 보일 수 있음.
- 영향
- 불안정한 학습
- 일반화 능력 저하로 새로운 데이터에 대한 예측 성능 저하
- 최저점을 찾아야 하지만 그에 맞는 수렴 속도가 감소

- 코드상에서 train을 할 때 learning rate(base_lr)를 지정하는데 이를 쉽게 이해하자면 한 발자국 폭이라고 생각하면 됨.
- 이 learning rate가 너무 크면 최저점을 찾아야 하는데 이동 폭이 너무 커 정확한 최저값을 찾기가 어려움.

- 반대로 learning rate가 너무 작아도 문제가 발생.

- 이 값의 변화정도에 따라 learning rate를 조절하면 됨.

- learning rate 조절에 관해 X 데이터를 먼저 선처리해야 할 때가 있음.

- gradient descent 그래프를 위에서 내려다 왔다고 생각하면 편함.
- 원형 가운데가 오른쪽 함수의 최저점이고, 어느 지점에서 출발하든 최저점에 도달하는게 목표임.
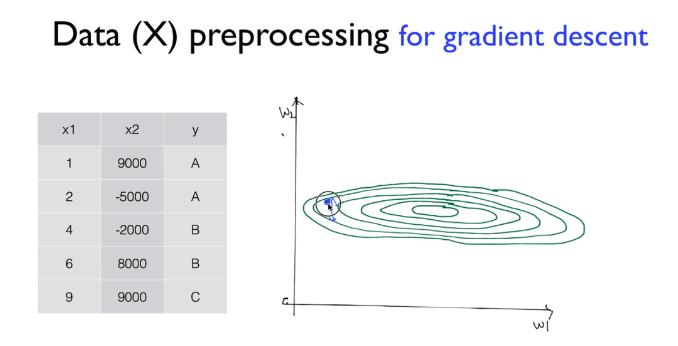
- 그런데 데이터가 부족하고 그 값의 차이가 크게 되면 그래프의 모양이 길죽한 타원의 모양으로 형성됨.

- 이런 그래프 형태일 때 learning rate를 조금만 크게 잡게 된다면 그래프에서 튕겨 나갈 수 있음.
- 이때 필요한 선처리가 바로 normalize라는 과정

- zero-centered data: 데이터의 중심이 0으로 가도록 하는 방법.
- normalized data: 지정한 범위 내에 항상 들어가도록 하는 방법.
- lr을 잘 설정한것 같지만 제대로된 학습이 안된다면 큰차이를 가진 데이터가 있는지, 그렇다면 선처리를 했는지 살펴보면 됨.

- 선처리는 standardization 이라는 normalize를 하면 되고, 수식의 아래 코드처럼 파이썬 코드상으로 간단히 처리할 수 있다.
Overfitting
- 모델이 훈련 데이터에 지나치게 적합하게 되는 현상
- 학습 데이터의 패턴뿐 아니라 데이터에 내재된 노이즈까지 학습하게 되는 상황
- 원인
- 모델에 너무 많은 매개변수를 가지고 있어 복잡도가 높음 → 훈련데이터에 완벽하게 맞춰짐.
- 과도한 깊이의 네트워크를 가지고 있음. → 복잡한 패턴을 학습할 수 있음.
- 적은양의 데이터. → 충분한 훈련이 되지 않으면 특이한 패턴이나 노이즈를 학습하게됨
- 너무 많은 에포크(epoch)동안 학습을 진행하면 모델이 훈련 데이터에 과적합되기 시작. → 일반화되지 않게 됨.
- 영향
- 훈련데이터의 노이즈나 특이한 패턴까지 학습하게 되면서 일반화 능력이 떨어지고 오버피팅으로 이어질 수 있음.


- 예를 들어 위처럼 model-1과 model-2가 있다고 가정 했을때, model-1이 좀 더 일반적인 모델이라고 할 수 있고 model-2는 학습용 데이터에만 맞춰져있어 실제로 사용할 때 다른 데이터에는 정확도가 떨어질 수 있는데 이를 overfitting 이라고 함.
- 해결 방법
- 더 많은 학습용 데이터.
- 중복된 feature 개수 줄이기.
- Regularization(일반화)

- weight을 너무 큰 값을 갖지 않도록 하면 좀 더 일반화 됨.

- + 뒤쪽에 수식 중 앞에 상수가 regularization strength 임.
- 상수 값이 0이면 regularization을 사용하지 않음, 값이 크면 클수록 regularization을 필요로 한다는 것.